|
Lab:
Surface Gravity and Weight
CHAPTER
8: UNIVERSAL GRAVITATION
download
lab
|
Applet Purpose: With this applet you may observe how weights differ from the
surface of one planet to another. In other words, it tells you that if
something weighs so much on the surface of one planet; it will weigh these
amounts on the surfaces of the other planets.
Click on the following link to access applet: http://library.thinkquest.org/27585/lab/sim_surface.html
How Do I Use It?
To use this applet simply enter a weight into the text box under one of
the planets and press the button that says "set" directly below
the box. The weights underneath all the other planets will automatically
change to be in accordance with what you entered.
Things to Try
Underneath Earth enter your weight and press set. What would
you weigh on the surface of Jupiter, the Moon or even the Sun? Fill in the
table below for each planet, moon, and sun based on your earth weight in
pounds.
Table
1. (My weight in pounds on):
|
Earth
|
Moon
|
Mercury
|
Venus
|
Mars
|
Jupiter
|
Saturn
|
Uranus
|
Neptune
|
Pluto
|
Sun
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculate your mass in kilograms. One kilogram is
approximately 2.205 pounds. Your mass = ___________ kg.
Your mass in the universe is a constant and would be the same on each planet,
moon, or star listed in the table.
Convert your weight in pounds to
Newtons
of force. Note: 1
pound = 4.448
Newtons
. State your weight in
Newtons
on each of the planets, moon
and sun. You will need to convert
pounds into
Newtons
for each value.
Table
2. (My weight in newtons on):
|
Earth
|
Moon
|
Mercury
|
Venus
|
Mars
|
Jupiter
|
Saturn
|
Uranus
|
Neptune
|
Pluto
|
Sun
|
|
|
|
|
|
|
|
|
|
|
|
|
Determine the acceleration of gravity on each planet, moon, and sun.
The pull of gravity is a force of attraction (called weight)
between two objects. One of the objects is usually larger than the other like a
planet, moon, or star. This force of gravity causes an object to be accelerated
toward the surface of the larger body. The force of gravity (in
Newtons
) equals the mass of the
smaller body times the gravitational acceleration caused by the larger body. F
= mg is the formula that illustrates this relationship. To find the
acceleration of gravity on these planets, moon and sun you need to solve this
equation for "g". The value "g"
will be the acceleration on or near the surface of each planet, moon, or sun.
Use this equation to find the acceleration on each surface in the table below.
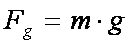 Rearrange
and you get
Rearrange
and you get
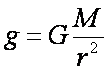
Using
Newton
ís
formula of Universal Gravity (chapter 8) and substituting it into the above
equation we end up with
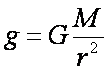
Acceleration
of gravity:
The acceleration of gravity on any
planet can be calculated from
Newton
's
formula of universal gravity where:
g = acceleration due to gravity (m/s2)
G
= universal gravitational constant (m3/kg/s2)
M
= mass of the body (kg)
r
= radius of the body (m)
The
value of G is known and has been estimated by scientists as:
G = 6.673 x 10-11 m3/kg/s2 in
the Metric system
Using
this relationship, we can solve for the acceleration due to gravity on any
planet so long as we know the planet's size. The acceleration due to gravity of
Earth, for example, is known to be about 9.81
m/s2 or 32.2 ft/s2. Let us verify this value by
plugging the Earth's mass (ME) and radius
(rE)
into the above equation.
ME = 5.98 x 1024 kg in the
Metric system
rE = 6.375 x 106 m in the
Metric system
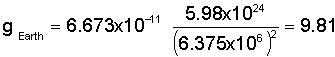
When
we do so, we find that the Earth's acceleration due to gravity is indeed about
9.81 m/s2. Use the table
below to calculate the acceleration due to gravity on the sun and planets below.
|
Acceleration
Due to Gravity Comparison
|
|
Body
|
Mass
[kg]
|
Radius
[m]
|
Acceleration
Due
to Gravity, "g" [m/s2]
|
g
/ g-Earth
|
|
Sun
|
1.99
x 1030
|
6.96
x 108
|
|
|
|
Mercury
|
3.18
x 1023
|
2.43
x 106
|
|
|
|
Venus
|
4.88
x 1024
|
6.06
x 106
|
|
|
|
Earth
|
5.98
x 1024
|
6.38
x 106
|
9.81
m/s2
|
1
|
|
Moon
|
7.36
x 1022
|
1.74
x 106
|
|
|
|
Mars
|
6.42
x 1023
|
3.37
x 106
|
|
|
|
Jupiter
|
1.90
x 1027
|
6.99
x 107
|
|
|
|
Saturn
|
5.68
x 1026
|
5.85
x 107
|
|
|
|
Uranus
|
8.68
x 1025
|
2.33
x 107
|
|
|
|
Neptune
|
1.03
x 1026
|
2.21
x 107
|
|
|
|
Pluto
|
1.40
x 1022
|
1.50
x 106
|
|
|
The
last column of the table compares the acceleration due to gravity of the body to
that of Earth. Divide the acceleration due to gravity on each planet by the
value of gravity on Earth. A small body like the Moon only exerts a
gravitational acceleration about 1/6th as strong as that of Earth while the
massive Sun generates an acceleration nearly 28 times that of Earth. Tiny Pluto,
meanwhile, only exerts about 4% the gravity of Earth.
This
information is also useful since it directly corresponds to how much an object
would weigh on the surface of each of these bodies.
Lab
modified from the following website:
http://www.hazelwood.k12.mo.us/~grichert/sciweb/weight.htm
http://www.aerospaceweb.org/question/astronomy/q0227.shtml
|