Chapter 5

INSTRUCTIONS:  In this homework assignment, we will be looking at problems involving motion in the y-direction (up and down).  In the world around us, gravity effects all objects motion when they are moving up or down.  You have already seen the series of equations from chapter 5 which describe uniform acceleration.  The letter “a” was used to represent acceleration in these equations.  When dealing with falling objects (or objects moving up) the letter “g” can be replaced in each of the equations.  Since we usually think of down being a “negative” direction, the acceleration due to gravity is equal to -g (a = -g).  The magnitude of gravity is 9.8 m/s2.  We assign a value to g of -9.8 m/s2 because this describes a direction downward.

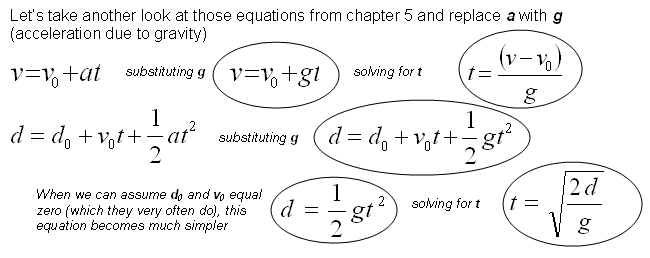
Definitions of each of the variables you see above:

v = This is the final velocity (or velocity of impact) (units = m/s)

v₀ = This is the initial velocity.  Use a positive (+) value if you initially throw something up.  Use a negative value (-) if you initially throw something down (units = m/s)  If the initial velocity is zero  (v₀ = 0), you can remove it from the equation.

a = acceleration.  When  solving problems using gravity, substitute g for a (remember g is a    constant at -9.8 m/s²)  This is because gravity always acts downward.  (units = m/s²)

d = final distance.  In the problems involving objects dropped, etc., d will represent the displacement in the y-direction.  It is positive (+) if the final position is above where you threw it.  It is negative (-) if the final position of the object is below where your threw it. (units = m)

d₀ = initial distance.  This is where the object started.  This value is very often = 0 (d₀ = 0).  In this case, you can remove it from the equation. (units = m)

t = This the time the object is in motion.  It is always positive.  If you find it to be negative, then you did something wrong!  (units = s)  

t₀ = This the initial time the object was put in motion.  Yes I know, you do not see this in any of the equations above.  That is because it was assumed in each that t₀ = 0, and was therefore eliminated from the equation.  REMEMBER → we arrived at each of the equations above from our two favorite equations of average velocity and average acceleration !

Motion Problems:  Remember, when solving the kinematics motion problems, always follow these three steps:

• Always start by writing down everything you know (the variables) and what they are asking you to find out (the unknown variable).  Always show the units!

• The next step is to draw a visual representation of the problem (a picture) to help you keep track of what is happening and what you are looking for. You then need to draw a coordinate system (an x-y board) to determine (+) or (-) values for your variables.  

• Now choose which equation fits your problem and plug in the values and solve for your unknown.

Solving Uniform Acceleration Problems Involving Gravity:  Let's look at some different types of questions you might be asked.   I will show you how to "lay out" each type of problem and then how to choose the correct equation to solve for your unknown.

Problem #1:  You drop a rock off the top of a tall building.  It takes 6.0 seconds to hit the ground.  How tall is the building?

FOLLOW THE STEPS BELOW TO SOLVE:  Make a drawing (a coordinate system) describing the problem and label all of the variables that you know.  Include velocities, distance, time and acceleration (gravity).

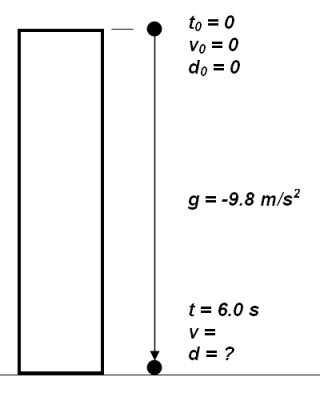
So what are you looking for?  That's right......final distance (d)

After writing down what you know and what you have been asked to find, look at the equations available to solve:

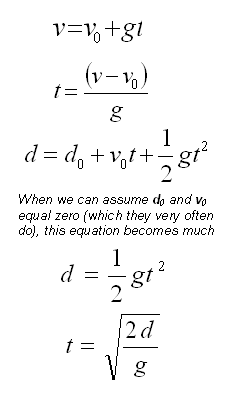
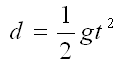
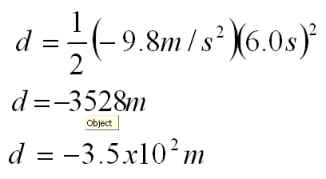
Since d0 and v0 equal 0, you can use the simple equation below to solve for d Plug in the values and solve Remember, distance can't be a negative number.  What this value tells you is displacement.  So the height of the building is (+) 3.5 x 102 m

Problem #2:  You drop a rock off the top of a 140 m tall building.  How long does it take before it hits the ground?

FOLLOW THE STEPS BELOW TO SOLVE:  Make a drawing (a coordinate system) describing the problem and label all of the variables that you know.  Include velocities, distance, time and acceleration (gravity).

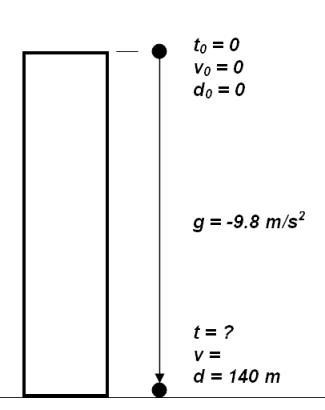
So what are you looking for?  That's right......final time (t)

After writing down what you know and what you have been asked to find, look at the equations available to solve:

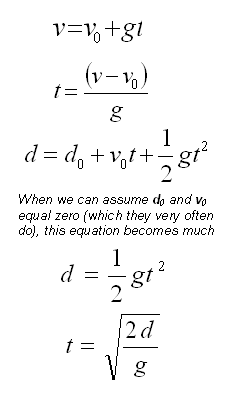
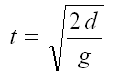
Since d0 and v0 equal 0, you can use the simple equation below to solve for t Plug in the values and solve

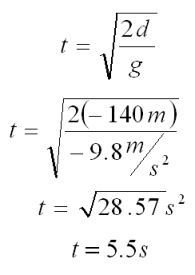
Problem #3:  You throw a rock off the top of a tall building with an initial velocity of 12 m/s.  It hits the ground going 33 m/s. How long does it take before it hits the ground?

FOLLOW THE STEPS BELOW TO SOLVE:  Make a drawing (a coordinate system) describing the problem and label all of the variables that you know.  Include velocities, distance, time and acceleration (gravity).

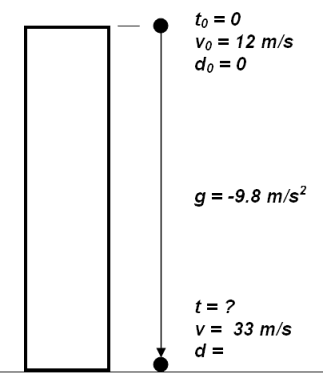
So what are you looking for?  That's right......final time (t)

After writing down what you know and what you have been asked to find, look at the equations available to solve. This time you have both initial and final velocity (v and v0)

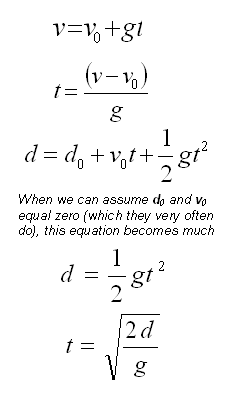
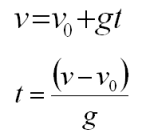
Since d0 and v0 do not both equal 0, you can not use the simplified equations as you did in the first two problems.  You must use the equation below.  Rearrange and solve for t Plug in the values and solve. Remember that velocities will both be (-) as well as gravity (they are both traveling DOWN!)

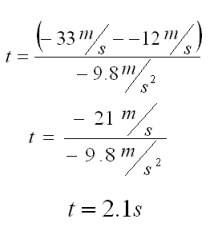
Problem #4:  You throw a rock as hard as you can up into the air.  It stays in the air a total of 8.0 seconds.  What was the velocity of the rock when you threw it?

FOLLOW THE STEPS BELOW TO SOLVE:  Make a drawing (a coordinate system) describing the problem and label all of the variables that you know.  Include velocities, distance, time and acceleration (gravity).

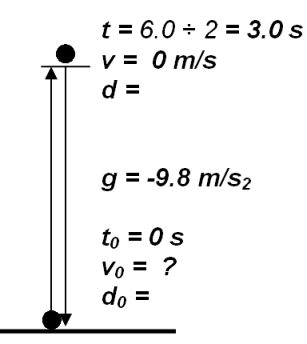
So what are you looking for?  That's right......initial velocity (v0)    Remember that it takes half the time to go up as high as it will get and exactly the same amount of time to return (gravity slows it down an equal amount on the way up as it speeds it up on the way back down) Also: it's velocity when it reaches the top will be 0 for a split second before it turns around and fall back down.

After writing down what you know and what you have been asked to find, look at the equations available to solve. This time you have both initial and final velocity (v and v0)

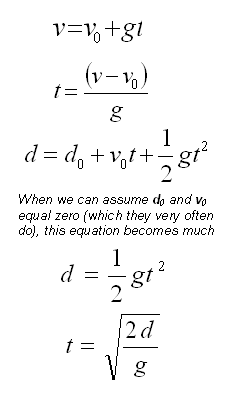
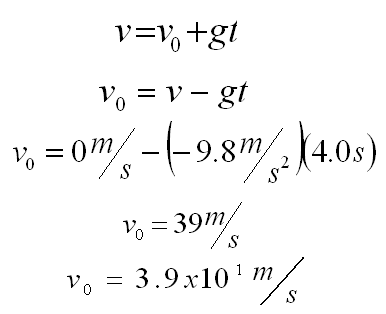
Since d0 and v0 do not both equal 0, you can not use the simplified equations as you did in the first two problems.  You must use the equation below.  Rearrange and solve for v0  Plug in the values and solve for v0  In this case, your value for velocity is (+).  That is because you are throwing it up (+), not down (-)!

Now it is your turn to try some practice problems.  

Practice Problem #1:  You drop a rock off the top of a tall building.  It takes 7.3 seconds to hit the ground.  How tall is the building?
Practice Problem #2:  You drop a rock off the top of a 85 m tall building.  How long does it take before it hits the ground?
Practice Problem #3:  You throw a rock off the top of a tall building with an initial velocity of 28 m/s.  It hits the ground going 44 m/s. How long does it take before it hits the ground?
Practice Problem #4:  You throw a rock as hard as you can up into the air.  It stays in the air a total of 12.0 seconds.  What was the velocity of the rock when you threw it?